Aplicando a Simulação de Monte Carlo no cálculo de Escalation

Uma boa definição dos custos do projeto é determinante para se obter sucesso na implantação de um empreendimento. Ao iniciar um projeto as estimativas de custos consideram moeda constante, materiais e mão de obra com uma data base definida. O orçamentista estima um valor de escalation para toda a duração do projeto, levando em consideração dados históricos disponíveis e projeções econômicas. Isto é ideal para condições econômicas normais e estáveis. A Simulação de Monte Carlo no cálculo do escalation é uma alternativa quando se tem um cenário de riscos, incertezas e variabilidade do mercado, mostrando os possíveis resultados e seus impactos, para que sejam avaliados e se tome as melhores decisões.

Introdução

Escalation é a provisão estimada para acréscimo nos custos de equipamentos, materiais, mão de obra, etc., devido ao possível aumento nos preços durante a implantação do projeto. Não deve ser confundida com Inflação. Uma das formas de se definir os índices a serem aplicados no cálculo do Escalation é o Método Determinístico, onde a partir de análise de índices históricos e previsões realizadas por entidades especializadas, determina-se os índices a serem utilizados no Projeto. A outra forma é o Método Probabilístico utilizando a Simulação de Monte Carlo. A Simulação de Monte Carlo é um método que simula os resultados das decisões e seus impactos possibilitando análises quantitativas das probabilidades de um evento acontecer.

Desenvolvimento

Escalation

A estimativa de investimento de um projeto é inicialmente desenvolvida considerando moeda constante (dólar, por exemplo), utilizando índices e preços de uma data- base comum. O preço unitário para os recursos de mão de obra e materiais são válidas para esta mesma data base.

O orçamentista estima antecipadamente um percentual de escalation para toda a duração do projeto, por categorias, tais como, equipamentos, commodities, mão de obra, etc. O cálculo é baseado em históricos econômicos ou em índice real de escalation dos anos anteriores.

São muitas as fontes de consulta para dados históricos da escalation de material/equipamentos e mão-de-obra. Exemplos: Banco de dados internos da empresa, Engineering News Record (ENR), AACE International Publications, Provincial Construction Decrees, etc. Para informação de outros países, câmaras de comércio, embaixadas e consulados podem fornecer estas informações.

Os índices de escalation de várias categorias podem ser reduzidos a três grandes grupos:

• Mão de obra
• Materiais e equipamentos
• Subcontratados

A média ponderada destes índices resulta no índice anual global de escalation. O índice anual é dividido em períodos conforme o fluxo de caixa (meses, trimestres, semestres, etc.). Em seguida o índice é aplicado às despesas por período no fluxo de caixa. A soma da verba de escalation em cada período fornece o escalation total projetado.

Sendo a contingência uma parte essencial da estimativa, está também sujeita a taxa de escalation. Consequentemente, a verba de escalation é a última linha apresentada, depois da contingência e antes da verba de risco, seguida somente do resultado final.

Visando facilitar a comparação dos custos reais versus custos estimados durante a implantação do projeto, é recomendado que a verba de escalation seja distribuída proporcionalmente e de acordo com a programação de despesa de cada item da estimativa. Portanto, os valores dos elementos do budget serão valores reajustados.

Esta metodologia fornece resultados suficientemente precisos e aceitáveis quando se tratando de condições econômicas normais. Para projetos de longa duração ou implantados em período de alta inflação, a metodologia pode ser modificada para atender as necessidades.

Simulação de Monte Carlo

Quando vamos definir os índices de Escalation, normalmente nos deparamos constantemente com incerteza, ambigüidade e variabilidade. E apesar de contarmos com acesso sem precedente à informação, não temos condições de prever o futuro de forma exata. A simulação de Monte Carlo permite ver todos os resultados possíveis de suas decisões e avaliar o impacto, possibilitando que se tome melhores decisões em situações de incerteza.

A simulação de Monte Carlo é programa que, através de uma técnica matemática, possibilita análises quantitativas das probabilidades de um evento acontecer e facilita tomada de decisão.

 A simulação de Monte Carlo fornece ao tomador de decisão uma gama de resultados possíveis e as probabilidades de ocorrências desses resultados de acordo com a ação escolhida como decisão. Ela mostra as possibilidades extremas — os resultados das decisões mais ousadas e das mais conservadoras — e todas as possíveis consequências das decisões mais moderadas.

Essa técnica foi usada inicialmente pelos cientistas que trabalharam na bomba atômica, e foi chamada de Monte Carlo como referência à cidade do Mônaco e seus cassinos. Desde sua introdução, na época da Segunda Guerra Mundial, a simulação de Monte Carlo tem sido usada para modelar uma variedade de sistemas físicos e conceituais.

A simulação de Monte Carlo efetua análise por meio da construção de modelos de possíveis resultados, substituindo com um intervalo de valores – uma distribuição de probabilidade – todo fator com incerteza inerente. Em seguida, ela calcula os resultados repetidamente, cada vez com outro conjunto de valores aleatórios gerados por funções de probabilidades. Dependendo do número de incertezas e dos intervalos especificados para elas, uma simulação de Monte Carlo pode ter milhares ou dezenas de milhares de recálculos antes de terminar. A simulação de Monte Carlo produz as distribuições de valores dos resultados possíveis.

 Ao usar distribuições de probabilidade, as variáveis podem apresentar diferentes probabilidades de ocorrência de diferentes resultados. As distribuições de probabilidade representam uma forma muito mais realista de descrever incerteza em variáveis de análises de risco. As distribuições de probabilidade mais comuns são:

Normal – também referida como “curva do sino”. O usuário simplesmente define a média aritmética ou o valor esperado e um desvio padrão para descrever a variações em relação à média. Os valores no meio, perto da média, são os que apresentam maior probabilidade de ocorrência.

Lognormal – nessa distribuição os valores são positivamente assimétricos ou distorcidos; não são simétricos como na distribuição normal. Ela é usada para representar valores que não passam abaixo de zero, mas que têm um potencial positivo ilimitado. Exemplos de variáveis representadas por distribuições lognormal: valores de imóveis, preços de ações, reservas petrolíferas.

Uniforme – nessa distribuição todos os valores têm probabilidade igual de ocorrência; o usuário simplesmente define o mínimo e o máximo.

Triangular – o usuário define os valores mínio, mais provável e máximo. Os valores ao redor do valor mais provável têm maior probabilidade de ocorrer. Variáveis que poderiam ser representadas por uma distribuição triangular: histórico de vendas passadas, por unidade de tempo, e níveis de estoque.

PERT – o usuário define o valor mínimo, mais provável e máximo, da mesma forma que na distribuição triangular. Os valores ao redor do valor mais provável têm maior probabilidade de ocorrer. Contudo, os valores que se encontram entre o valor mais provável e os dois extremos têm maior probabilidade de ocorrência do que na distribuição triangular, isto é, os extremos não são tão enfatizados. Exemplo do uso de uma distribuição PERT: descrever a duração de uma tarefa em um modelo de gerenciamento de projeto.

Discreta – o usuário define valores específicos que podem ocorrer e a probabilidade de cada um deles. Um exemplo poderia ser os resultados de um processo judicial: 20% de chance de decisão judicial positiva, 30% de chance de decisão judicial negativa, 40% de chance de um acordo e 10% de chance do julgamento ser encerrado por motivo jurídico.

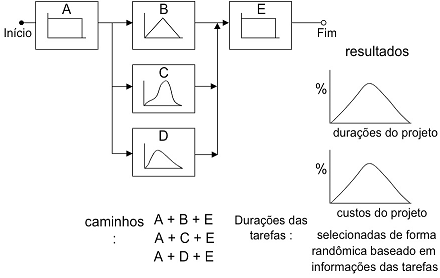
Durante uma simulação de Monte Carlo, as amostras dos valores são obtidas aleatoriamente das distribuições de probabilidade de inputs (entradas). Cada conjunto de amostra é chamado de iteração, e o resultado produzido a partir da amostra é registrado. A simulação de Monte Carlo faz isso centenas ou milhares de vezes, e o produto disso é uma distribuição de probabilidade dos resultados possíveis. Dessa forma, a simulação de Monte Carlo fornece um quadro muito mais abrangente do que poderá acontecer. A figura 01 abaixo mostra um organograma que facilita o entendimento do método empregado pela simulação.

Fig 01 – Organograma representativo das interações da simulação de Monte Carlo

A simulação de Monte Carlo proporciona uma série de vantagens, em relação à análise determinística ou de estimativa de um único ponto.

• – Resultados probabilísticos: Os resultados, além de mostrar o que poderia ocorrer, também mostram a probabilidade de cada ocorrência.
• – Resultados gráficos: Graças aos dados gerados pela simulação de Monte Carlo, é fácil criar gráficos dos diferentes resultados e suas probabilidades de ocorrência. Isso é importante para poder comunicar as informações obtidas às partes interessadas.
• – Análise de sensibilidade: Como a análise determinística é baseada em apenas alguns casos, é difícil ver quais são as variáveis que mais afetam os resultados. Com a simulação de Monte Carlo, é fácil ver que inputs têm maior efeito nos resultados finais.
• – Análise de cenário: Nos modelos determinísticos, é muito difícil modelar diferentes combinações de valores para diferentes inputs, para ver os efeitos em cenários efetivamente diferentes. Ao usar a simulação de Monte Carlo, o analista pode ver exatamente quais inputs tinham quais valores na ocorrência de determinado resultado. Essa informação é valiosíssima para aprofundar a análise.
• – Correlação de inputs: Na simulação de Monte Carlo, é possível modelar relações interdependentes entre as variáveis de input. Isso é importante para fins de exatidão, para representar como, na realidade, quando certos fatores sobem outros também sobem ou caem, conforme o caso.

Existem no mercado atualmente alguns softwares que executam a simulação de Monte Carlo, um deles é o @Risk 6, que conforme a imagem a seguir, retrata de maneira eficiente e clara, os resultados desejados.

Fig. 02 – Software de Simulação Monte Carlo @Risk 6

Conclusão

Definir o valor do Escalation de um Projeto utlizando Método Deterministico, aplicando-se índices disponíveis no mercardo é bastante simples. No entanto, quando se trata de projeto de longo prazo, esta estimativa fica pobre. Para estes Projetos uma análise mais apurada pode ser desejada e então o Método Probabilístico como o de Monte Carlo apresenta um resultado mais confiável, porém a sua aplicação prática pode representar um significativo esforço. O tempo e o custo para este esforço é muito variável, dependendo das habilidades e conhecimentos dos desenvolvedores e os usuários a respeito dos métodos e ferramentas de Monte Carlo, o status e a complexidade da base de dados, software a ser utilizado e assim por diante.

Referências

•  AACE International, Recommended Practice – 68R-11: Escalation Estimating Using Indices and Monte Carlo Simulation – TCM Framework: 7.6 – Risk Management
• Simulação de Monte Carlo –    http://www.palisadebr.com/risk/monte_carlo_simulation.asp
• 2007 AACE International Transactions – Est.08 – Escalation: How Much is Enough? – Glenn Butts, CCC – PEER REVIEWED
• 2007 AACE International Transactions – RISK.03 – The Monte-Carlo Challenge: A Better Approach  -John K. Hollmann, PE CCE.
• Confiabilidade e Otimização de Estruturas de Concreto Armado – http://slideplayer.com.br/slide/1595953.
• Software de Simulação Monte Carlo @Risk – http://www.palisade-br.com/risk

Sobre os Autores:

Eder de Castro Pereira, Engenheiro Mecânico, MBA em Gestão de Negócios, com mais de 30 anos de experiências, atuando em empresas locais e multinacionais, nas áreas de mineração, metalúrgicas, eletromecânicas e autopeças. E-mail para contato: eder.castro@snclavalin.com

Marcos Paulo Ponciano Gomes, Engenheiro de Produção, formado a 3 anos,atuação em como analista de performance entre 2010 e 2012 na Sotreq S/A , e atualmente atuo como analista de tecnologia industrial na área de manutenção industrial na empresa Comau do Brasil, localizada na fabrica da Fiat em Betim. E-mail para contato: gomes.ponciano@gmail.com  

Tiago Araújo Rocha Nascimento, Engenheiro de Produção com ênfase em Planejamento Energético pela UFOP, formado a 08 anos, de Trainee a Gerente de Logística pela Athos Farma, responsável por um Centro de Distribuição no Nordeste e nos últimos 3 anos como Diretor de Operações da E3R, com sede em Belo Horizonte atendendo demandas de eficiência energética no Brasil. E-mail para contato: tiago@e3r.com.br

Contexto: o presente trabalho é resultado de pesquisa realizada com alunos da 7a Turma de Engenharia de Custos e Orçamento – AUEG –  com a coordenação do Prof. Ítalo Coutinho do IETEC. O presente trabalho tem como base a norma da AACE – Recommended Practices – http://www.aacei.org/resources/rp: 68R-11: Escalation Estimating Using Estimating Indices and Monte Carlo Simulation.

Se você tem comentários, sugestões ou alguma dúvida que gostaria de esclarecer, aproveite o espaço a seguir.