Publicado em 08/02/2016
RESUMO
O trabalho discute a aplicação da metodologia “Simulações de Monte Carlo”, aplicadas à área de gerenciamento de projetos. A cultura hoje dominante está baseada em um modelo determinístico e reducionista, mas a realidade se aproxima, devido às incertezas, de um modelo probabilístico. A utilização da Simulação de Monte Carlo, baseada apenas no algoritmo matemático, quando aplicada em gerenciamento de projetos, mostra-se por demais limitada. O importante não é a simulação da variação matemática do parâmetro de uma variável, mas sim, entender os fenômenos que podem afetar esta variável e como estes fenômenos influenciam o desenvolvimento de um projeto. E desta maneira, poder atuar preventivamente nesses fatores. A necessidade de uma explicação mais detalhada da teoria das incertezas em projetos, tornou este artigo um pouco extenso. Sendo assim, ele foi dividido em duas partes, como segue:
Parte 1 – Teoria das incertezas em projetos e a Simulação de Monte Carlo pelo MS-Excel.
Parte 2 – Aplicação da Simulação de Monte Carlo em projetos. Em Breve (29/02)
INTRODUÇÃO
Como discutido em artigos anteriores, e parte transcrito neste para retomar a discussão das vantagens da utilização de modelos probabilísticos, é muito comum ouvir-se que “Planejar” significa visualizar o futuro. Como poucos têm o dom de pitonisa, este autor entende ser mais adequada a seguinte definição: “Planejar” significa moldar o futuro.
O problema reside na maneira que essa atividade é executada, pois nosso pensamento é linear, cartesiano e determinístico. Usam-se dados determinísticos do passado para inferir o futuro e desta maneira, projeta-se um futuro determinístico. Esse modo de projeção não deixa de ser importante, é um bom ponto de partida. O problema é que o futuro não é determinístico, pois as incertezas existem.
Não se educa para que as pessoas pensem probabilisticamente e assim, cria-se dificuldade de aceitação de que os projetos apresentam enormes incertezas. E ainda tenta-se simplificar as ações, quebrar o projeto em partes diminutas e sem atentar, as pessoas são levadas a aplicar técnicas lineares em problemas complexos. Agindo assim, muitas vezes não se enxerga o inter-relacionamento entre as atividades e decisões são tomadas baseando-se apenas na seguinte equação: um problema, uma solução isolada.
Nos projetos ocorrem poucos fatos de natureza determinística, pois na maioria das vezes não se tem absoluta certeza do que ocorrerá no futuro e, nestas condições de incertezas, aplicar técnicas determinísticas e reducionistas para explicar fenômenos complexos tem apresentado resultados decepcionantes.
Algumas metodologias existentes no mercado contribuem para que as análises das incertezas sejam mais abrangentes. Como existe a dificuldade de enxergá-las, podem levar os projetos a situações de riscos indesejáveis. Por outro lado, metodologias como o PERT, Simulações de Monte Carlo, adaptação do Front-End/Plannig, do IPA (Independent Project Analysis), com suas fases FEL1, 2 e 3 e a Metodologias do Diagrama de Fases da Petrobras, auxiliam na identificação das incertezas e riscos, em cada etapa do projeto.
De acordo com Moschin, no livro S.Exa.,O Parzo (2012), essas metodologias apresentam diferenças significativas e precisam ser consideradas no planejamento, como segue:
- Existem diferenças nas estimativas das durações para uma mesma atividade estipulada por métodos diferentes.
- É possível eliminar as folgas desnecessárias sem prejudicar a execução das tarefas.
- Um gerenciamento e um acompanhamento criterioso das atividades interferem de maneira positiva para a eliminação dessas folgas.
- Existe remédio para as doenças do planejamento e, devido a isso, é possível obter ganhos em cronogramas elaborados pelas empresas.
FUNDAMENTAÇÃO TEÓRICA
Metodologia para delineamento de Cronograma
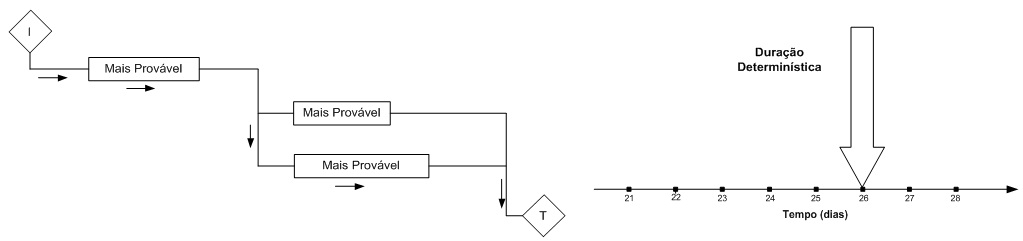
Para delineamento de cronogramas é muito usada a metodologia CPM – Método do Caminho Crítico, que consiste em se trabalhar com durações determinísticas. E, nestas condições, o resultado é uma duração discreta, única.
Figura 1 – Exemplo de diagrama de rede com durações determinísticas
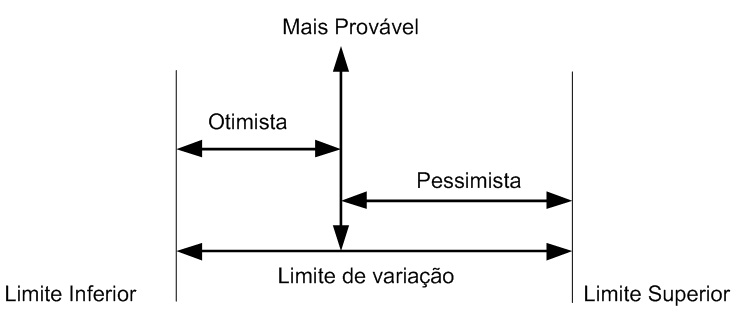
No método do Caminho Crítico considera-se que a variável “mais provável” é uma constante, ou seja, um valor discreto. Mas, na realidade esta variável pode oscilar entre os limites inferiores e superiores, como exemplificado na figura 2. E toda insegurança é embutida neste valor discreto. Quanto mais insegurança, mais o valor se aproxima do valor pessimista.
Figura 2 – Exemplo de limites de oscilação de uma variável aleatória
Essa rigidez contribui para a acomodação da equipe. A busca pela excelência é deixada de lado. O sucesso é cumprir o prazo determinístico e esquece-se das folgas desnecessárias embutidas.
Proposta de Mudança de Paradigma
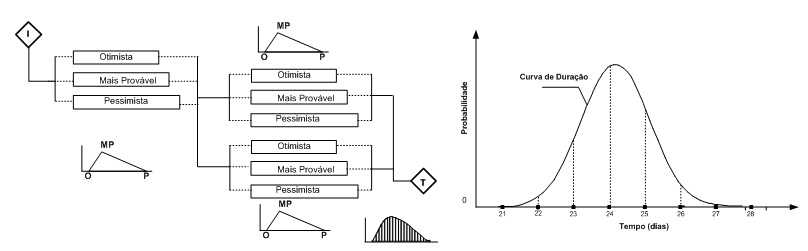
A proposta é usar metodologias que atiçam a mente a enxergar as incertezas e fazer delas uma aliada na busca das oportunidades de ganho e consequentemente, da excelência.
Figura 3 – Exemplo de combinação de durações – Fonte: Livro S. Exa., O Prazo, Qualitymark Editora, RJ, 2012.
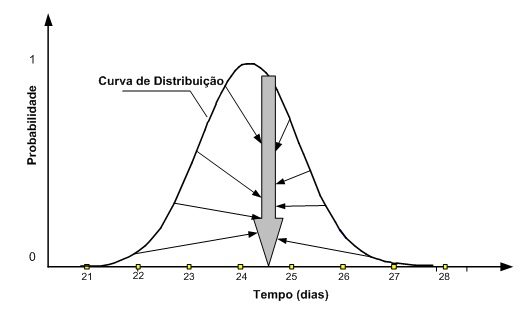
Figura 4 – Exemplo gráfico da atuação das forças em um projeto com durações determinísticas
A realidade é probabilística e normalmente usa-se uma modelagem determinística, que fornece um ponto na curva de distribuição. Toda energia é consumida para fazer acontecer este prazo determinístico, como mostra a figura 4. Para as tarefas que apresentem algum atraso, usam-se as práticas do paralelismo ou da aceleração de atividades, com aumento de recursos, etc. e para as tarefas adiantadas, o ritmo é reduzido. Ou seja, o prazo determinístico torna-se a verdade absoluta e a meta é o cumprimento deste prazo. Na sequência deste artigo serão discutidos os inconvenientes e a perda da produtividade.
Simulações de Monte Carlo
A Simulação de Monte Carlo foi proposta pelos matemáticos Von Neumann, Ulam e Fermi, durante o projeto de desenvolvimento da bomba atômica (Manhattan). Estudaram a possibilidade de se utilizar um método, que simulasse a natureza probabilística relacionada à difusão do nêutron em certos materiais. A lógica do método já era conhecida há muito tempo em artigo do cientista Lord Kelvin em que discutia as técnicas de Monte Carlo, nas equações de Boltzmann. O nome Monte Carlo é uma homenagem à cidade de Monte Carlo e seus famosos cassinos.
Matematicamente, a técnica de Monte Carlo consiste em gerar valores aleatórios para cada distribuição de probabilidades dentro de um modelo com o objetivo de produzir centenas ou milhares de cenários.
Em linguagem de projetos, significa a simulação matemática de diversas possibilidades de cenários, obedecendo-se as restrições do projeto. Ou seja, trabalha-se com informações operacionais de um sistema real.
Usando-se as Simulações de Monte Carlo é possível obter facilmente informações importantes sobre o projeto, como:
- Qual a probabilidade do projeto terminar no prazo negociado.
- Qual a probabilidade do projeto terminar no custo negociado.
- Qual a probabilidade do projeto terminar na data X.
- Quais as tarefas mais críticas.
- Qual a data mais provável do projeto terminar.
- Qual o custo mais provável a ser alcançado.
- Quais as tarefas que participaram mais vezes no caminho crítico.
Exemplo de um churrasco
Quantos quilos de carne serão consumidos em um churrasco para 100 pessoas?
Pode-se adotar uma estimativa grosseira e discreta, como segue:
Estimativa de comparecimento – 90%
Estimativa de consumo médio por pessoa – 350gr
= 100 x 0,9 x 0,35
= 31,5 kg de carne
Notem que este valor representa uma média. E como chegar a um valor mais próximo da realidade, que reflita as incertezas associadas ao evento?
Opção 1 – Repetir esse churrasco, para essas mesmas 100 pessoas, nas mesmas condições ambientais, por 10.000 vezes. Anotar o consumo real em cada churrasco e depois traçar uma curva de distribuição. Naturalmente que isso é impraticável.
Opção 2 – Simular matematicamente o consumo de carne dessas 100 pessoas, em 10.000 churrascos. Ou seja, fazer oscilar a variável estudada dentro de determinados limites, seguindo-se as regras matemáticas.
Base matemática – geração de números aleatórios para a variável.
Geração de números aleatórios
- Dispositivos físicos, como roleta, dados, moedas, etc.
- Tabelas de números aleatórios
- Processos matemáticos e computacionais
Simulação de Monte Carlo pelo programa MS-EXCEL
Passos
1 – Escolha da variável. No caso, o consumo de carne
2 – Acessar no Excel
- “Dados”
- “Análise de Dados”
- “Geração de Números Aleatórios”
3 – Escolha da distribuição que melhor represente este evento. Como não se conhece o comportamento da variável, adota-se uma distribuição, por exemplo, a Uniforme, preencher os campos no pop-up “Geração de Números aleatórios” e rodar.
4 – Acessar no Excel o pop-up do “Histograma” e traçar o gráfico.
- “Dados”
- “Análise de Dados”
- “Histograma”
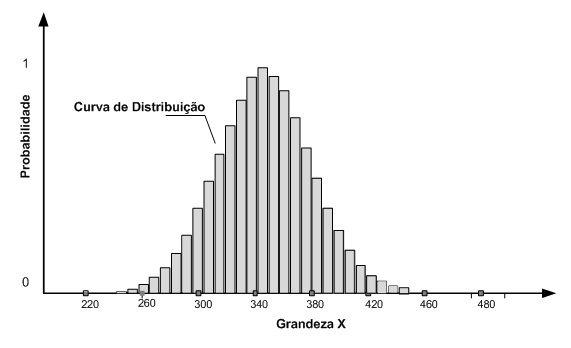
Resultado esperado: Uma curva de distribuição. É importante verificar que o valor mais provável adotado na estimativa acima, faz parte da curva de distribuição. É possível também determinar qual a probabilidade desse valor ocorrer. E para cada valor de consumo, é possível associar uma probabilidade.
Figura 5 – Curva da distribuição
O resultado apresentado tem como base a aplicação de método matemático puro, ou seja, os fatores responsáveis pela oscilação da variável são desconhecidos. Torna-se assim importante a realização de uma análise de riscos e a elaboração de um plano de respostas, com todas as medidas preventivas identificadas. Por isso foi denominada apenas de uma ferramenta matemática. E em projetos, o uso desta ferramenta é muito importante e conduz para melhores resultados, desde que adaptada à metodologia dedicada aos projetos, como discutido nos itens a seguir.
Na segunda parte deste artigo, será discutida a aplicação das Simulações de Monte Carlo em projetos.
REFERÊNCIAS BIBLIOGRÁFICAS
- Barcaui, André B. et alii, Gerenciamento do Tempo em Projetos, 1a edição, editora FGV, 2006.
- Mosquim, Puch, Oliveira, Trabalho de Conclusão de Curso, FGV-BI-Institute – Campinas-2008.
- Moschin, John, S.Exa., O Prazo, 1a edição, Editora Qualitymark, 2012.
- Moschin, John, Gerenciamento de Paradas de Manutenção, Editora Brasport, 2015.
- PMBOK: Um Guia do Conjunto de Conhecimentos em Gerenciamento de Projetos. Quinta edição, PMI – Project Management Institute, Inc., Pensilvânia, USA, 2014.
- Ribeiro, Carlos Augusto B., Apostila de Gerência de Tempo em Projetos, FGV, 2006.
- Programa Primavera Analysis Risk, Oracle
Sobre o Colunista: João Carlos Mosquim, Engenheiro Civil e de Equipamentos, MBA em Gerenciamento de Projetos e pós-graduação em Gestão de Pessoas, especialização em Controle da Qualidade e certificação PMP do Project Management Institute. Foi membro da Banca Examinadora do Prêmio Nacional da Qualidade, Membro da Comissão de Eletricidade da ABRAMAN, Avaliador/auditor em processos integrados de gestão, Normas NR-10, ISO 9001, 8800, 14001, 18001. Desenvolveu atividades na Petrobras nas áreas de empreendimento, manutenção, automação de sistemas de produção e elétricos e planejamento de rotina e paradas. Palestrante em webinares do PMI-USA, PMI-SP, Fixe Consulting, autor de artigos e trabalhos técnicos apresentados em 5 Congressos Mundiais de Manutenção – ABRAMAN. Hoje é sócio-diretor da MKM CONSULTAITIS, empresa de consultoria e treinamento nas áreas de Gerenciamento de Projetos, Riscos, Paradas e Indicadores de Desempenho, e como professor de MBA na Pragma Academy Brasil.
E-mail de contato: mkmconsultatis@gmail.com
Se você tem comentários, sugestões ou alguma dúvida que gostaria de esclarecer, aproveite o espaço a seguir.







obrigado!
Gratidão pelo seu compartilhamento de tão relevante saber.
Parabéns pela didática e clareza na explicação e exemplificação.