Publicado em 16/06/2015
Nos últimos anos, os veículos aéreos não tripulados do tipo quadrirotor ou quadcopter, têm tido destaque especial nas pesquisas de sistemas robóticos, principalmente devido a versatilidade de sua navegação poder ser tanto em ambientes externos ou internos. Para que um aeromodelo impulsionado por quatro rotores possa se manter em equilíbrio com relativa precisão, mesmo que em voo pairado, é necessário um algoritmo de controle que estabilize o sistema dinamicamente, impedindo que ele colapse devido a uma perturbação ou devido ao somatório de dinâmicas geradas por seu próprio peso. Existem várias técnicas de controle para o voo dos quadcopters, para o trabalho proposto elabora-se uma malha fechada utilizando um algoritmo equacionado pela lei de controle PID. Para o feedback da planta, utiliza-se circuito integrado de mensuramento inercial, composto de acelerômetro, giroscópio e magnetômetro para monitorar-se a orientação angular, e utiliza-se sonar para monitorar-se a altitude. Dentro destes parâmetros estruturais e teóricos, propõe-se passar pela pesquisa, simulação, projeto, construção, e, à prática.
Pelo fato deste trabalho tratar de um objetivo que solicita relativa interdisciplinaridade de conhecimentos, partimos das conceituações teóricas, matemática e computacional, como forma de nortear a sequência de opções mais adequadas a um bom resultado. Deste ponto em diante, os esforços estão na transposição das soluções teóricas e virtuais para o sistema real, através das seguintes etapas:
- a) Diagramação mecânica e cinemática da estrutura física do aeromodelo, suas características sobre capacidade de sustentação e estabilidade;
- b) Equacionamento matemático do somatório de dinâmicas físicas envolvidas no voo de uma aeronave em seus 6 graus de liberdade;
- c) Parametrização do algoritmo de interfaceamento sensores-microcontrolador;
- d) Construção do circuito de desenvolvimento agregado ao microcontrolador, estrutura parcial do aeromodelo com apenas 2 rotores e seus respectivos ESCs (Electronic Speed Controllers) e da plataforma de teste para sustentação em modelo de balança;
- e) Simulação em ambiente computacional e otimização das equações dinâmicas e seus referentes coeficientes de ganho;
- f) Implementação do algoritmo de controle e sua utilização em plataforma de um grau de liberdade para captura de dados dos sensores, cálculo dos parâmetros do filtro digital de Kalman e das respostas parciais da planta;
- g) Complementação da estrutura física para seus quatro rotores, implementação da malha fechada para voo pairado e novo estágio de otimização;
- h) Análise de resultados e conclusões.
A metodologia empregada em cada etapa será descrita a seguir.
1.1 Cinemática e mecânica
Pré requisito ao equilíbrio do conjunto, há a capacidade de sustentabilidade da altitude do voo. No caso do quadcopter, esta sustentação é alcançada através das hélices. São equipamentos de propulsão acoplados aos motores que convertem a energia da rotação em translação, empurrando o fluido à sua volta. As hélices são formadas por conjuntos de asas, que ao serem rotacionadas geram uma diferença de pressão entre suas superfícies superior e inferior, segundo explicitam a 3ª lei de Newton e o princípio de Bernoulli.
O comportamento de uma hélice pode ser baseado em 3 parâmetros; o coeficiente de thrust cT (coeficiente de sustenação), coeficiente de potência cP e raio da hélice r, p a densidade do ar e w a velocidade angular, que permitem calcular as seguintes equações 1 e 2 (RODRIGUES, 1964).
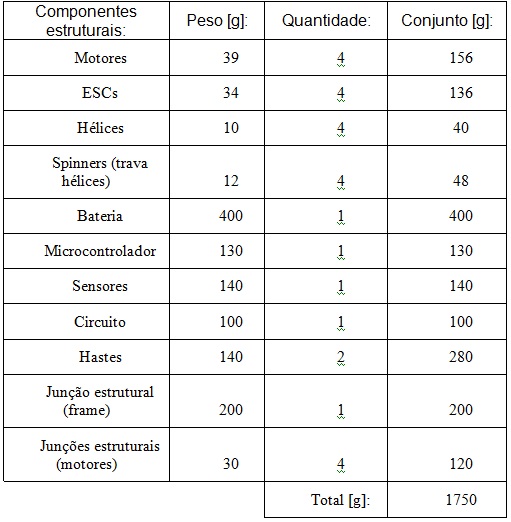
Através destas equações é possível observar que T (força de impulso) e Pp (potência de propulsão) aumentam consideravelmente com o aumento do diâmetro, e por consequência o consumo de energia também, diminuindo a autonomia do sistema. A análise da melhor configuração para as hélices deve ser baseada em particularidades do aeromodelo, como, potência e faixa de eficiência dos motores, tipo de bateria, tempo de resposta e peso. Abaixo, uma estimativa do peso do conjunto na tabela 1:
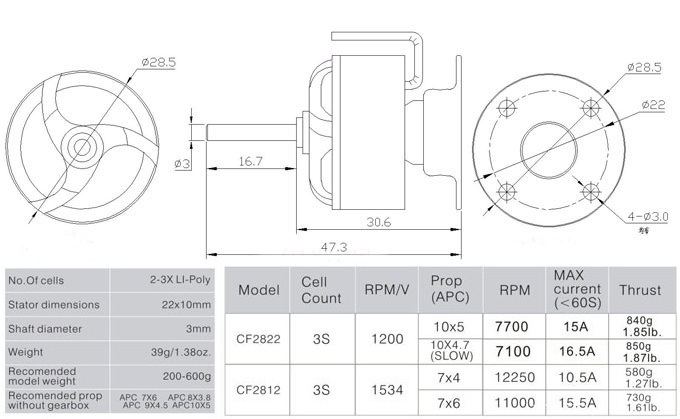
Sendo assim toda a estrutura do protótipo poderá alcançar 1750 gramas, peso adequado à capacidade dos motores CF2822 equipados com hélices de 10 polegadas de diâmetro por 5 polegadas de passo, segundo recomendações do fabricante, como visto na figura 1.
Figura 1. Especificações dos motores: Yin Yan Model, 2014
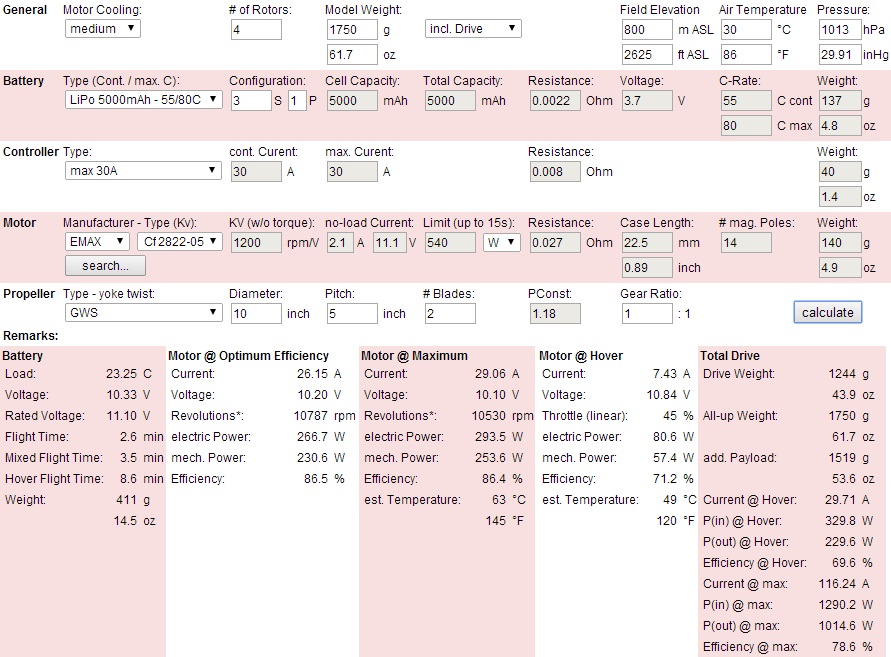
Uma análise mais completa das condições de funcionamento do conjunto de propulsores, tanto para modo de voo em sustentação quanto para regime de empuxo máximo, foi feita pelo site eCalc, com índice de incerteza de dez por cento. Quanto à autonomia, cerca de três a 8 minutos de voo ao aeromodelo, dependendo do tipo de voo (eCalc, 2014). Eficiência, temperatura, corrente e demais dados constantes na figura 2.
Figura 2. Simulação de parâmetros eCalc : Site eCalc
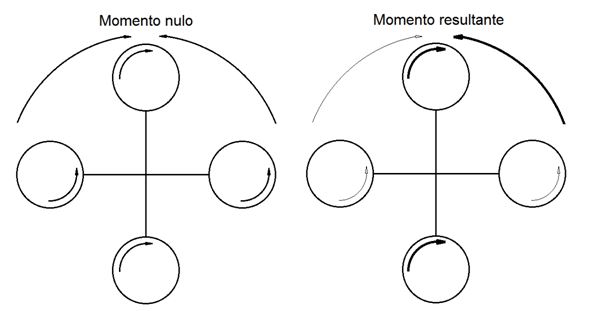
A estrutura de um quadcopter é baseada em dois eixos cruzados contendo um propulsor em cada extremidade. Sendo que, seu centro de massa deve estar coincidente ao seu centro geométrico. O par de rotores de um eixo gira em sentido contrário ao par do eixo transverso. De forma que os momentos de reação gerados pelo giro dos motores tendem a se anular e aumenta-se a estabilidade, como na figura 3.
Figura 3. Somatório de momentos (guinada): Elaborado pelos autores
No caso da rotação da estrutura em Z, por guinada, é possível alterar o somatório de empuxo entre os pares de propulsores e gerar um momento total resultante.
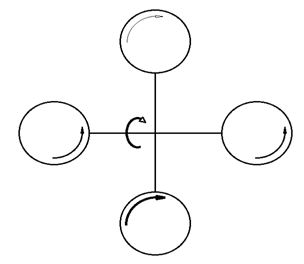
Rotações em torno de seus próprios eixos, por arfagem (eixo Y) ou rolagem (eixo X), podem ser obtidas pela variação do empuxo médio em apenas um dos pares de rotores (figura 4).
Figura 4. Rolagem ou arfagem: Elaborado pelos autores
Os movimentos de translação, ou, mudanças de velocidade linear podem ser obtidos pela inclinação do conjunto seguida do incremento do empuxo total.
Como forma de se iniciar os estudos da cinemática do sistema, uma estrutura que modela um grau de liberdade, foi estudada de forma a propiciar a obtenção das respostas do sistema contendo apenas dois propulsores (figura 5).
Figura 5: Estrutura de modelamento em um grau de liberdade: Elaborado pelos autores
1.2 Equacionamento matemático
O equacionamento da dinâmica de um corpo rígido, mesmo que em voo pairado, envolve múltiplos níveis de interpretação. Em seus seis graus de liberdade, um corpo rígido, pode transladar ao longo de seus eixos referenciais e rotacionar em torno destes mesmos eixos.
Quanto à rotação, uma das formas mais simples de se descrever a posição de um corpo, é através de três ângulos independentes que fazem referência ao espaço Euclidiano tridimensional, estes são os ângulos de Euler.
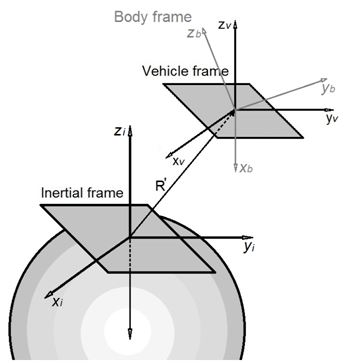
Definindo como origem de um sistema de coordenadas fixo, também chamado de inercial, um ponto na superfície da Terra (desconsiderando seu movimento orbital), e, um outro sistema de coordenadas móvel (vehicle frame), que se desloca em translação junto ao corpo rígido, pode-se obter o vetor posição do corpo em relação ao sistema inercial. Um terceiro frame acompanha as rotações do corpo em relação ao sistema móvel, o body frame (figura 6).
Figura 6: Coordenadas de múltiplos corpos: Elaborado pelos autores
A relação, entre as coordenadas do sistema móvel e do sistema fixo, é definida através de transformações lineares de translação e rotação.
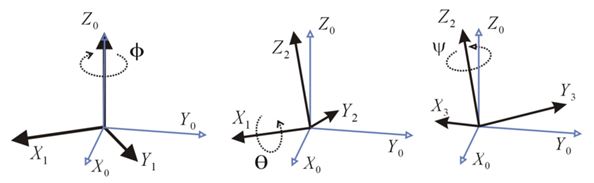
Como parâmetros para os eixos de rotação, os ângulos são Φ (em Z), θ (em X) e Ψ (em Y) (figura 7).
Figura 7: Ângulos de Euler: McCormick, 1995
Sendo â um ângulo qualquer dentre os três ângulos de rotação, ρ o vetor posição e R a matriz de rotação, a equação geral de transformação das rotações é:
Assim, a e matriz de representação da rotação para Ψ (guinada) fica:
A matriz de representação da rotação para θ (arfagem) fica:
A matriz de representação da rotação para Φ (rolagem) fica:
Finalmente, considerando os três eixos, tem-se a relação entre o frame do corpo e o frame do veículo:
Sendo a matriz de rotação:
Sendo p, q e r, as taxas de rotação do corpo ao longo de x, y e z do frame do corpo. Sendo u, v e w as velocidades do corpo em x, y e z do frame do corpo. Sendo x’, y’ e z’ no frame inercial. A equação da posição em relação à velocidade fica (BOUABDALLAH, 2007):
A transformação das magnitudes dos ângulos absolutos Φ, θ e Ψ, em taxas de variação angulares p, q e r, não é trivial, pelo fato dessas quantidades serem definidas em diferentes sistemas de coordenadas. As velocidades angulares estão frame do corpo, enquanto as posições angulares estão no frame do veículo. Considerando que as velocidades angulares são pequenas, pode-se relacionar p, q e r às derivadas no tempo de Φ, θ e Ψ, através da matriz de rotação, vista na equação 9 (BEARD, 2008):
Quanto ao empuxo, a força efetiva T, ou Thrust Force, sentida pelo quadcopter, é o somatório das quatro forças de seus rotores. Sendo essa força consequência das características do conjunto propulsor, ou fator de Thrust, tido como cT, e da velocidade angular (equação 10).
Decompondo T em função das direções dos eixos, pode-se discretizar as equações de forças (equações 11, 12 e 13).
1.3 Simulação em ambiente computacional
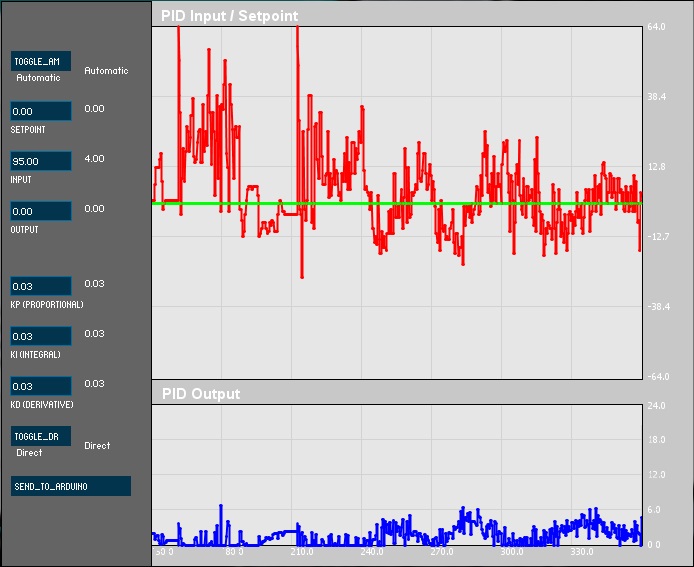
Como passo inicial, foi implementado diretamente ao compilador Arduino, disponibilizado pela Atmel, um algoritmo de controle PID clássico, à estrutura composta por apenas dois propulsores. De forma a se obter um sistema pouco agressivo e capaz de se estabilizar, em seu um grau de liberdade, os coeficientes de proporcionalidade, integrativo e derivativo, foram de 0.03 (todos os três). Na figura 8, pode-se perceber o set-point de zero grau como a reta horizontal, a resposta como inclinação variando em torno do set-point, e, a escala de saída em um dos motores.
Figura 8: Curvas de entrada e saída: dados experimentais
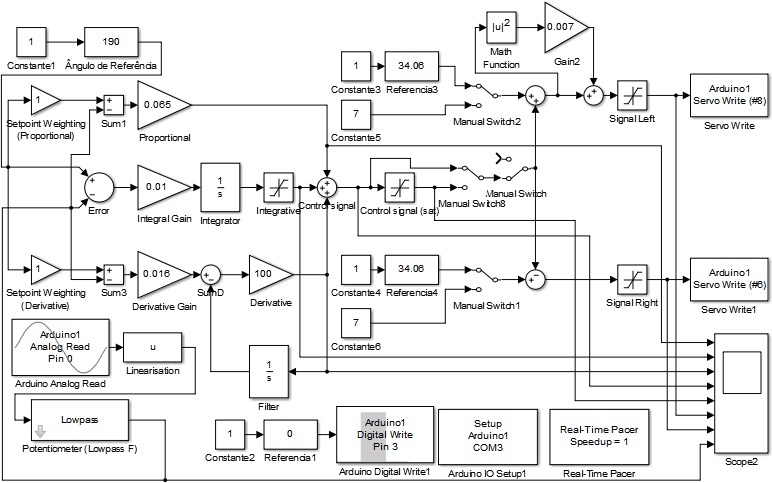
Uma resposta melhor veio através da ferramenta computacional Simulink, contida no software MatLab, após a filtragem mais sintonizada de leitura do sensor e da equalização dos motores, feita por uma função exponencial em um dos motores, foi possível o alcance de um sistema rápido, que nos trouxe apenas uma oscilação após cada entrada degrau. O diagrama no Simulink pode ser visto na figura 9.
Figura 9: Diagrama em um grau Simulink: Elaborado pelos autores
A partir da mesma disposição de simulação, foram obtidas respostas satisfatórias para o controle das respostas na rotação em torno do eixo “Z” (somatório de momentos) e propulsão (somatório de empuxos dos atuadores).
1.4 Parametrização do algoritmo de sensoriamento
Neste projeto, se optou pelo módulo de voo 10DOF (Ten Degrees Of Freedom) modelo GY80, como equipamento de sensoriamento principal. O GY80 é uma pequena placa de circuito eletrônico SMC (Surface Mounted Components), que conta com acelerômetro, giroscópio, magnetômetro e barômetro. Devido à relevante quantidade de sensores acomodados em uma mesma plataforma, a comunicação deste equipamento com o MCU (Micro Controller Unit) é feita através do protocolo I2C (Inter Integrated Circuits). Basicamente, este código trabalha com dois tipos de sinais entre os CIs, o sinal de clock (gerado pelo CI mestre) que sincroniza a troca de informações, e o sinal de dados, este bidirecional.
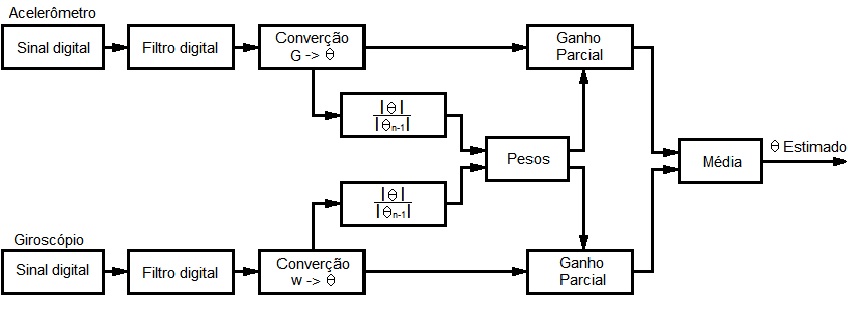
Para estimativas de posicionamento, o sistema deve ser realimentado com sinais de rotação e translação. Neste caso, a fusão de sensores entre acelerômetro e giroscópio é uma boa opção para leitura angular. A principal intenção, em uma fusão de sensores, é promover a iteração entre as magnitudes medidas por cada sensor individualmente, e correlacioná-las de forma a manter uma resposta aceitável, mesmo que ocorram erros em alguma leitura, tornando o sistema menos sensível e mais preciso.
Integrado ao módulo de voo há o acelerômetro digital de três eixos ADXL345, com capacidade para perceber acelerações de -g à +g (aceleração da gravidade). Tomando como premissa que o acelerômetro esteja exatamente ao centro da estrutura, pode-se dizer que variações de ângulo em torno de seus próprios eixos não seriam percebidas pelo mesmo. Mas devido ao alto índice de vibrações do sistema, gerado pelos motores, há ainda medições indesejadas sendo captadas. Considerando então, que filtros digitais (assunto que abordado em outro tópico) serão aplicados de forma à reduzir as leituras equivocadas, podemos teorizar sobre um cálculo que descarta estas vibrações.
Sabendo-se que a aceleração da gravidade é de 9.81 m/s2, o somatório das componentes trigonométricas deste vetor pode estimar a inclinação.
O giroscópio (Angular Rate Sensor), modelo L3G4200D, faz medidas da velocidade de rotação. Devido à necessidade de contínuas integrais no tempo, para transformar a leitura da velocidade de angular em deslocamento angular, pequenos desvios são incorporados à leitura, o que torna o giroscópio pouco preciso ao longo do tempo.
Como forma de superação de grande parte das fontes de imprecisão características de cada sensor, a fusão sensorial pode ser entendida com um grau mínimo de complexidade, como na figura 9:
Auxiliando o acelerômetro e o giroscópio, temos a bussola digital MCS (Magnetic Compass Sensor), modelo HMC5883L, pode-se obter o ângulo de Azimute, pela sua percepção do campo magnético da Terra (equação 16).
Como feedback da altitude, pode-se ainda, com o sensor de pressão, modelo BMP085 (Pressure sensor), estimar a altitude com relativa precisão. Tendo como off-set a altitude a memória da pressão do ponto de decolagem, é possível gerar um parâmetro de altitude da aeronave a cada tempo.
1.5 Circuito de desenvolvimento
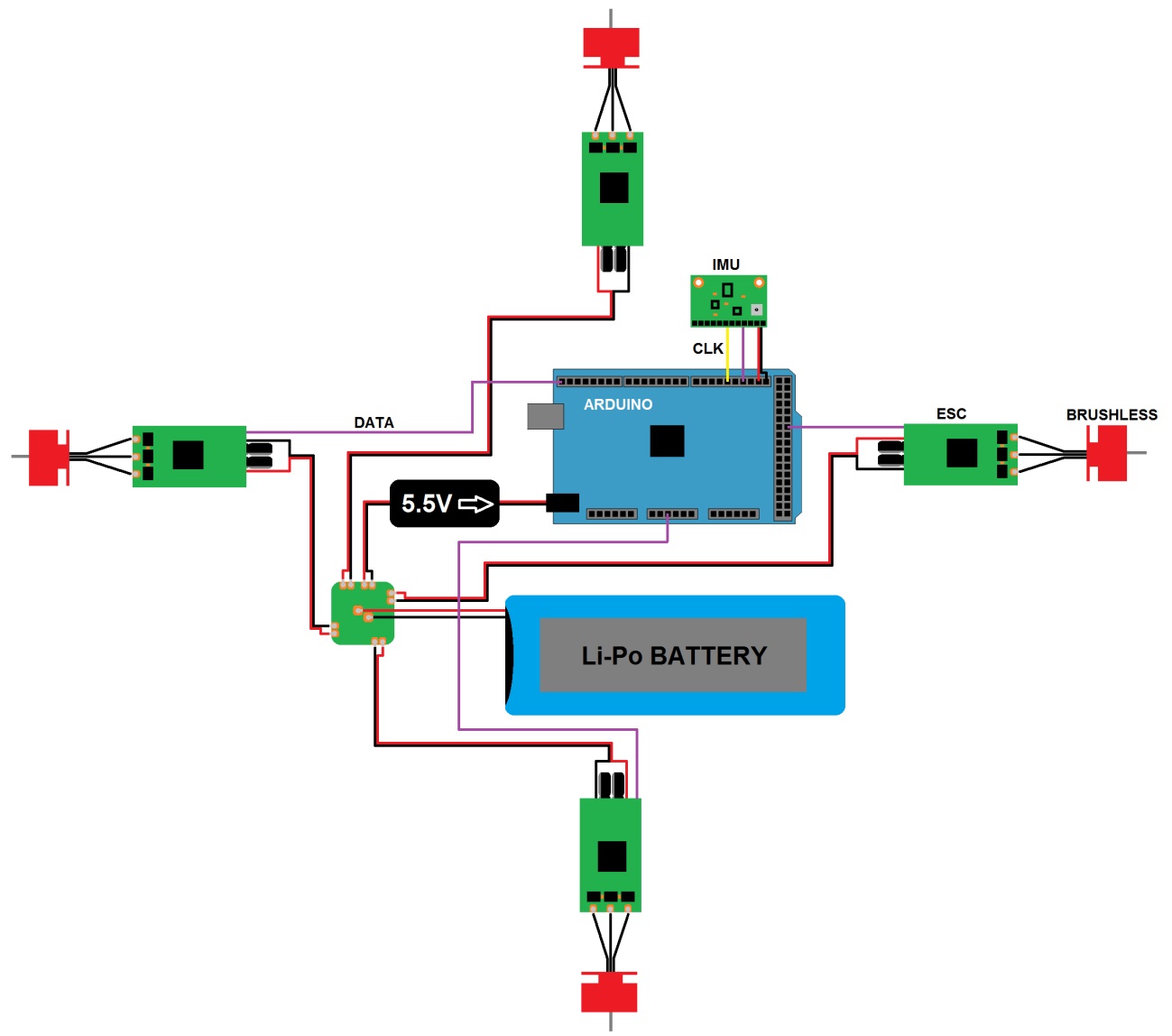
O esquema elétrico-eletrônico de um aero-modelo do tipo quadrirotor, como na maioria dos sistemas autômatos, é construído basicamente em prol da interface entre controlador, atuadores, sensores e bateria. O circuito de desenvolvimento deste protótipo se assemelha a este modelo. A bateria fornece energia ao regulador de tensão, que alimenta o microcontrolador com 5 volts, este por sua vez, energiza os sensores. Esta mesma bateria fornece energia aos motores através dos ESCs (Electronic Speed Controllers) (figura 10):
Figura 10: Circuito de desenvolvimento: Elaborado pelos autores
Os motores brushless necessitam de uma alimentação caracterizada pela sobreposição de três ondas senoidais defasadas de 120 graus uma da outra. De forma que, cada uma destas ondas alimente um grupo diferente de enrolamentos. Esses motores não possuem sensores que facilitem o monitoramento de sua posição angular ou velocidade, de forma, que sua alimentação eficiente se torna uma tarefa bastante complexa.
Os ESCs se encarregam de alimentar os motores, conforme recebem o sinal de controle do microcontrolador, através do fio chamado data. Este sinal é feito através do código PWM (Pulse-Width Modulation), que ao ter seu duty-cicle variado, varia a resposta do ESC.
O Arduino Mega, é um microcontrolador de 8 bits da Atmel, 16MHz de clock e 256KB de memória flash. Possui ainda, 54 pinos de comunicação com o exterior, dos quais, 15 podem ser saídas PWM, e 16 entradas analógicas. Sua comunicação com o módulo de voo, ou IMU, é feita través do código serial I2C, sendo realizada por apenas dois fios. Onde, um destes é utilizado para determinação do clock de comunicação, feito pelo dispositivo master, e o outro é utilizado para troca de comandos e dados. Assim, o microcontrolador pode determinar os parâmetros de sensoriamento e receber as magnitudes das leituras sensoriais.
1.6 Algoritmo de controle
O código de controle foi fundamentado com base nas simulações e aplicado em prol da estrutura física em sua íntegra, composta de seis graus de liberdade. Este algoritmo encontra-se ainda em fase de revisão, por estar sendo “transcrito” do formato em diagrama de blocos do ambiente Simulink para a linguagem C.
Destaca-se nesta fase a importância de se considerar os movimentos translacionais em função de “X” e “Y“, devido ao drift gerado pelo processo de equilíbrio do voo pairado. Este assunto é de interesse destes autores para uma revisão futura, quando possivelmente será tratado de forma a se realizar estimativas dos deslocamentos em função das inclinações e da propulsão em cada somatório de momentos.
1.7 Estágio de otimização
A otimização de um sistema, está relacionada a diversos fatores de análise e estudo. Dentre estes fatores, para este projeto relevam-se, as determinações, dos parâmetros das equações de controle e suas curvas de resposta, dos coeficientes de controle, dos coeficientes dos filtros de sinais de sensoriamento, da repetição das simulações em ambiente computacional e dos testes de campo.
Como forma de facilitar o ajuste em campo das variáveis que fazem parte do controle, foram instalados potenciômetros às entradas analógicas do microcontrolador, em que suas leituras representavam estas variáveis, em suas devidas escalas.
Não houve necessidade de variar o equacionamento em prol da queda de energia armazenada na bateria.
A equalização dos motores, de forma a deixá-los com respostas semelhantes em função das amplitudes das entradas aplicadas e das faixas de potência variadas, foi o estágio de otimização de mais primordial importância para garantir o controle do protótipo.
2 Conclusão
A pesquisa da teoria e o entendimento, de boa parte de todo assunto científico abordado neste trabalho, não garantem alcançar um resultado ótimo do sistema. Trata-se de um sistema em que seu único amortecimento é a viscosidade dinâmica do ar atmosférico se opondo aos graus de liberdade da estreita estrutura. Sendo sua estabilização quase que exclusivamente dependente do conjunto de variações conjugadas dos impulsos de seus quatro propulsores.
As longas hastes metálicas, equipadas por motores que chegam a sete mil rotações por minuto, trazem para estrutura uma magnitudes de frequências de excitação e natural que podem ser aproximadas pelos harmônicos gerados pelos motores, em diversas de suas faixas de rotação. Esta semelhança entre as frequências natural e de excitação, geram ressonância. A amplificação das oscilações do corpo rígido dificultam relevantemente a leitura dos sinais de interesse do acelerômetro, pois este é o fenômeno de que se trata sua sensibilidade, a taxa de variação da velocidade. O que gera um nível relevante de dificuldade ao controle, pois o funcionamento do sistema interfere em seu próprio sensoriamento. Tema que está entre as maiores dificuldades deste trabalho.
A iteração entre filtragem dos sinais, equacionamentos das transformadas de unidades e as aplicações das técnicas de fusão das leituras através de um filtro dinâmico, integram o tratamento dos sinais. A aplicação do filtro de Kalman, por si só, é um desafio considerável. Alcançar uma boa relação entre seus parâmetros e sua implementação, não é tarefa trivial. Outra desvantagem que se percebe ao analisar o algoritmo é o tempo computacional gasto, sendo sua aplicabilidade a um sistema limitada pelo tempo de processamento da unidade de controle digital. Pois, os tempos de cálculo, saída e atuação, devem ser menores que o tempo entre uma perturbação exógena e sua alteração real do sistema. Um loop lento do controlador pode inviabilizar a necessária resposta a um sistema agressivo.
De forma geral, a desenvoltura no alcance de soluções, que foi estabelecida durante o processo de confecção deste protótipo, indica que há possibilidade de sucesso no tema de enfoque do título. Pois foi possível o controle de voo pairado para quatro graus de liberdade utilizando-se a Teoria de Controle Clássica (PID). Contudo, o resultado é um sistema que contém uma faixa de atuação em voo limitada se comparado à um quadcopter implementado sob um controle não estacionário, como Lógicas Fuzzy ou Redes Neurais.
Referências:
- Abbasi E., Mahjoob M. J. & Yazdanpanah R., 2013. Controlling of Quadrirotor UAV Using a Fuzzy System for Tuning the PID Gains in Hovering Mode. School of Mechanical Engineering, University of Tehran, Iran.
- Beard, R. W, 2008. Quadrirotor dynamics and control. Brigham Young University.
- Bouabdallah, Samir, 2007. Design and Control of Quadrirotors with Application to Autonomous Flying. École Polytechnique Fédérale de Lausanne. Lausanne.
- eCalc. Multicopter Calculator. Diponível em: <http://www.ecalc.ch/xcoptercalc.php?ecalc&lang=en>. Acesso em: 19 apr. 2014.
- Mccormick, W. Barnes, 1995. Aeronautics and Flight Mechanics. New York, Wiley, 2 ed.
- Rodrigues, José, 1964. Aeromodelismo teórico e prático. Serviço de Publicações da Mocidade Portuguesa.
- Yin Yan Model 2014. Manual E-Max CF2822. Disponível em: <http://www.http://www.yinyanmodel.com/en/ProductView.asp?ID=58>. Acesso em: 20 apr 2014.
Sobre os Autores:
Daniel de Castro Ribeiro Resende, é Engenheiro Mecânico com linha de formação em Mecatrônica especializado em programação de firmwares e malhas de sensoriamento. Possui experiência em motores Ciclo Otto e Powertrain automotivo. E-mail para contato: engenheirodanielribeiro@gmail.com
Pedro Américo Almeida Magalhães Júnior, Possui graduação em Bacharelado em Engenharia Elétrica pela Universidade Federal de Minas Gerais (1989), graduação em Bacharelado em Ciência da Computação pela Pontifícia Universidade Católica de Minas Gerais (1989), especialização em Engenharia Civil pela Fundação Educacional Minas Gerais (1993), mestrado em Engenharia Elétrica pela Pontifícia Universidade Católica de Minas Gerais (2001) e doutorado em Engenharia Mecânica pela Pontifícia Universidade Católica de Minas Gerais (2009). Criador do software VCN-Visual Cálculo Numérico. Tem experiência na área de Matemática e Engenharia, com ênfase em Análise Numérica e Análise Estrutural, atuando principalmente nos seguintes temas: análise matemática, cálculo numérico, equações diferenciais, métodos estatísticos, elementos finitos, mecânica experimental, processos industriais, gerenciamento de projetos, metrologia ótica, engenharia de software, resistência dos materiais, fadiga mecânica. E-mail para contato: paamj@oi.com.br
Nicolas Ives Roque Pacheco, Pontifícia Universidade Católica de Minas Gerais. E-mail para contato: nickirp@gmail.com.br
Se você tem comentários, sugestões ou alguma dúvida que gostaria de esclarecer, aproveite o espaço a seguir.
Ainda não recebemos comentários. Seja o primeiro a deixar sua opinião.

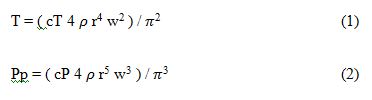


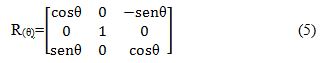
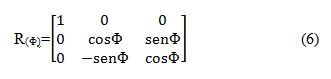
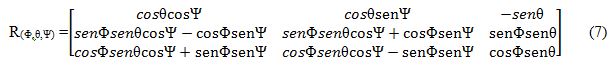
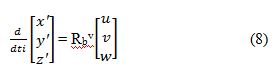

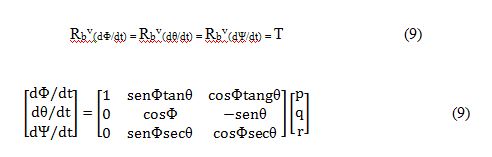
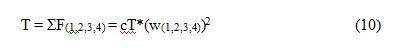







Deixe uma resposta